Region Decomposition: Stock exchange trade pricing¶
Financial exchanges and other venues like 'dark pools' and MTFs operate notoriously complex trading systems. In this notebook, we'll use Imandra's Region Decomposition feature to enumerate all of the 'edge-cases' of a component of the SIX Swiss trading logic (as described here).
In particular, we will use Imandra to:
- Model a fragment of the logic (the one dealing with fill price determination)
- Decompose the state-space of the logic to enumerate all of its regions (or 'edge cases')
- Transform the results to English-like prose
- 'Slice' the state-space with additional logic constraints
- Generate concrete instances for each of the regions
Region Decomposition is a novel technique for analysis of algorithms' state-spaces and is available via Imandra's "Reasoning as a Service" platform. It is inspired by Cylindrical Algebraic Decomposition (CAD) but is lifted to general algorithms written in OCaml or ReasonML (Imandra supports both, but this notebook uses OCaml). Imandra leverages many recent breakthroughs in formal verification to make this happen. This functionality is already relied upon in production by leading financial institutions, so please reach out to us if you would like to incorporate this into your products or development workflow. For more information, please see the documentation page.

Modelling trading venues¶
At Imandra, we've pioneered a formal approach to modelling financial venues as infinite state machines. No doubt you've heard of finite state machines (or FSMs) - these are commonly used to describe logic of a streetlight or some other engineering artefact with a finite number of states. The problem with venues that operate in the real world is that they may be in a virtually infinite number of states (think of all the possible sequences of incoming messages, operator settings, outside market dynamics, etc.).
Full description of this methodology is outside the scope of this notebook, but it's useful to keep in mind as you read through the following example. We'll also use 'simplified' types (e.g. representing time as integers and prices as reals) - interested readers should check out our public GitHub repositories and publications for full type definitions.
Order type definitions¶
Our first step is to define type for orders:
type order_type = Market | Limit | Quote
type order = {
order_id : int;
order_type : order_type;
order_qty : int;
order_price : real;
order_time : int;
}
There are instances when we would not be able to determine a fill price (e.g. when the book is empty). To account for this, we'll make fill_price type support both cases.
(* There are instances when the fill price may not be calculated at all. *)
type fill_price =
| Known of real
| Unknown
(* An order book contains lists of buy and sell orders. *)
type order_book = {
buys : order list;
sells : order list
}
Auxiliary functions¶
We'll define some helper functions which we'll use later on. The trading guide specifies that price of a fill may be influenced by the best and second best orders in the book (symmetrically buys and sells).
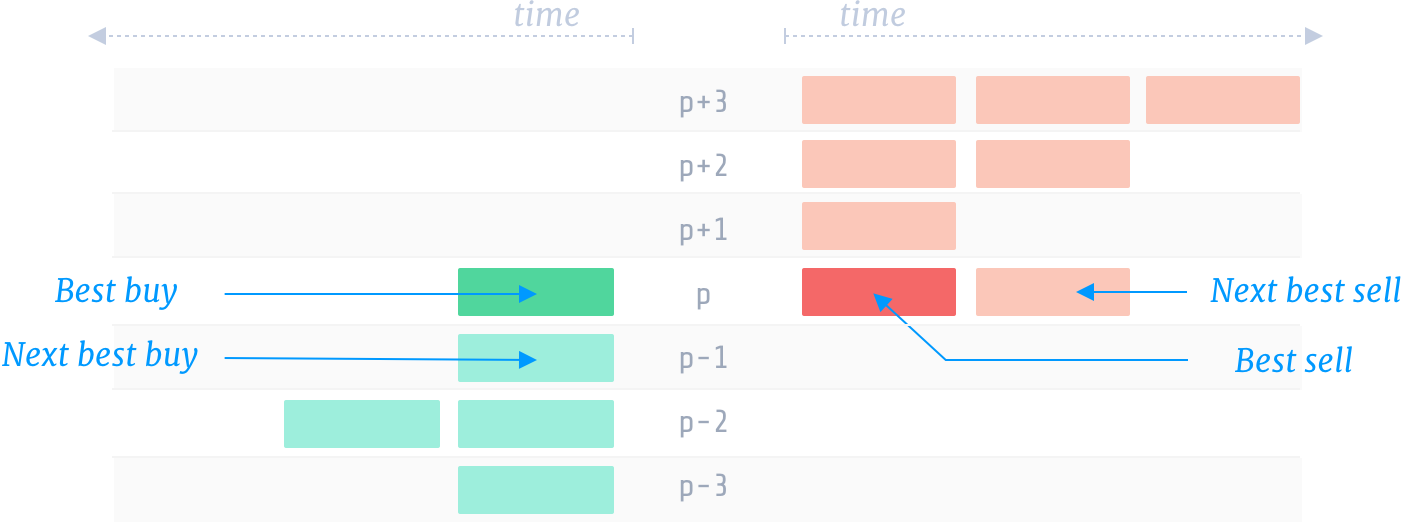
Please note: the notion of 'best' orders in the code below is with respect to an order ranking criteria which is omitted in this notebook for brevity. We assume that the orders are already sorted with respect to this criteria. So, the 'best' buy order is the first order in the list. Sorting of order books is an interesting topic in itself - in 2015 we won (1st place out of more than 620 companies) the UBS Future of Finance FinTech Challenge where we demonstrated that the ranking criteria used in UBS ATS (as it was described in the SEC filing) was not transitive, leading to potentially significant violation of regulatory directives and "best-ex" rules. For more information, please read our whitepaper.
(* Determine whether order 1 or 2 is older. *)
let older_price o1 o2 =
if o1.order_time > o2.order_time
then o2.order_price else o1.order_price
(* Return the best buy order of the book. *)
let best_buy (ob : order_book) =
match ob.buys with
| x :: _ -> Some x | [] -> None
(* Similarly, return the best sell order of the book. *)
let best_sell (ob : order_book) =
match ob.sells with
| x::_ -> Some x | [] -> None
(* Second-best buy order of the book *)
let next_buy (ob : order_book) =
match ob.buys with
[] -> None | [o1] -> None
| o1 :: o2 :: _ -> Some o2
(* Second-best sell order *)
let next_sell (ob : order_book) =
match ob.sells with
[] -> None | [o1] -> None
| o1 :: o2 :: _ -> Some o2
Pricing logic¶
Now that we have defined all of the necessary types and auxiliary functions, it's time to define the actual price-determining logic - match_price function that accepts two parameters:
ob- order book as defined aboveref_price- reference price of the exchange. This refers to the last stable fill price that the exchange traded on. The exact definition is more nuanced, but for our purpose - just think of it a form of an 'anchor' that's used to determine fill prices when an order book doesn't contain enough information.
Here's the main function for our exercise:
let match_price (ob : order_book) (ref_price : real) =
(* Select the best buy and sell order of the order book (if they exist) *)
let bb = best_buy ob in
let bs = best_sell ob in
match bb, bs with
(* Now we'll match on values of `bb` and `bs`. We're using OCaml's option types -
explicitly having a value of `None` when no `bb` or `bs` order exists. *)
Some bb, Some bs ->
begin
match bb.order_type, bs.order_type with
(* When we're matching Limit/Limit or Quote/Quote orders, then
the outcome is simply limit price of the older order. *)
| (Limit, Limit) | (Quote, Quote) -> Known (older_price bb bs)
(* Logic gets more nuanced, however, when *)
| (Market, Market) ->
if bb.order_qty <> bs.order_qty then Unknown
else
(* need to look at other orders in the order book *)
let bBid = match (next_buy ob) with
Some bestBuy ->
if bestBuy.order_type = Market then None
else Some bestBuy.order_price
| _ -> None in
let bAsk = match (next_sell ob) with
Some bestSell ->
if bestSell.order_type = Market then None
else Some bestSell.order_price
| _ -> None in
begin
match bBid, bAsk with
| (None, None) -> Known ref_price
| (None, Some ask) ->
if ask <. ref_price then Known ask
else Known ref_price
| (Some bid, None) ->
if bid >. ref_price then Known bid
else Known ref_price
| (Some bid, Some ask) ->
if bid >. ref_price then Known bid
else
if ask <. ref_price then Known ask
else Known ref_price
end
| (Market, Limit) -> Known bs.order_price
| (Limit, Market) -> Known bb.order_price
| (Quote, Limit) ->
if bb.order_time > bs.order_time then
(* incoming quote *)
begin
if bb.order_qty < bs.order_qty then Known bs.order_price
else if bb.order_qty = bs.order_qty then
match (next_sell ob) with
| None -> Known bb.order_price
| Some ord -> Known ord.order_price
else Unknown
end
else
(* existing quote's price is used *)
Known bb.order_price
| (Quote, Market) ->
if bb.order_time > bs.order_time then
(* incoming quote *)
begin
let nextSellLimit = next_sell ob in
if bb.order_qty < bs.order_qty then Known bs.order_price
else if bb.order_qty = bs.order_qty then
match nextSellLimit with
| None -> Known bb.order_price
| Some ord -> Known ord.order_price
else Unknown
end
else
(* The quote's price is used *)
Known bb.order_price
| (Limit, Quote) ->
if bb.order_time > bs.order_time then
begin
(* incoming quote *)
if bs.order_qty < bb.order_qty then
Known bb.order_price
else
if bb.order_qty = bs.order_qty then
match (next_buy ob) with
| None -> Known bs.order_price
| Some ord -> Known ord.order_price
else
Unknown
end
else
(* existing quote's price is used *)
Known bs.order_price
| (Market, Quote) ->
if bb.order_time > bs.order_time then
begin
(* incoming quote *)
if bs.order_qty < bb.order_qty then Known bb.order_price
else if bb.order_qty = bs.order_qty then
(match (next_buy ob) with
| None -> Known bs.order_price
| Some ord -> Known ord.order_price
)
else Unknown
end
else
(* The quote's price is used *)
Known bs.order_price
end
| _ -> Unknown
Now that we've defined match_price, let's try it out. We'll start by declaring 4 instances of different orders for us to experiment with later:
let order1 = {
order_id = 1;
order_type = Market;
order_qty = 1000;
order_price = 0.0;
order_time = 123;
}
let order2 = {
order_id = 2;
order_type = Quote;
order_qty = 250;
order_price = 12.56;
order_time = 125;
}
let order3 = {
order_id = 3;
order_type = Limit;
order_qty = 250;
order_price = 40.0;
order_time = 125;
}
let order4 = {
order_id = 4;
order_type = Market;
order_qty = 250;
order_price = 0.0;
order_time = 125;
}
We'll now evaluate match_price with these new orders. Notice that we'll define order_book value inline when we call the function.
Region Decomposition of match_price¶
We've tried a few examples and it already feels that there are many ways match_price can behave. From the type definitions, we know that there are virtually infinitely many possible inputs into match_price. So how can we enumerate these distinct 'edge cases'?
This is what Region Decomposition is designed to do.
To decompose the state-space of match_price, we'll use Modular_decomp.top command. Notice that while our types and the actual code was entered in Imandra's logic mode, we'll now switch to program mode. The results of decomposition will be reflected into program mode so we may use the full power of OCaml language to utilise the results.
Analysis of the results¶
The regions Imandra produces cover the entire behavior of match_price function. In Jupyter Notebooks we've created hierarchical Voronoi diagrams for their easier exploration. In this widget, all of the leafs are distinct regions (e.g. R[2]), while edges are constraints that are shared with regions below. So, (1) denotes a group of regions all sharing the constraint (List.hd ob.buys).order_qty = (List.hd ob.sells).order_qty. If you click on the top-left edge, the right pane will display information about this region, namely that there are 3 Direct sub-regions and 23 Contained Regions.
Refinement and pretty-printing¶
The results displayed are terse - the default printer returns all of the low-level information that Imandra generates. This is intended - you may wish to process all or some of this data.
To make processing this data easy, we have created Imandra-tools - a library with transformers for easy manipulation and printing of this data.
Let's try to render the results in something closer to English. For example, a reference to the first buy order within the logic would be described as List.hd ob.buys, or in the correct underlying type notation as Funcall (Var "List.hd", [ FieldOf (_, "buys", Var "ob")]). We would much rather see 'First buy order' rather than List.hd ....
The following code will use Imandra-tools to condense the region constraints and make them more "readable":
#program;;
open Imandra_tools;;
module PPrinter = Region_pp.PPrinter;;
module Refiner = struct
open Region_pp
open PPrinter
(* This function will be used to traverse the regions' data (constraints and invariants) and convert them to humanly readable text *)
let walk (x : node) : node = match view x with
| Funcall ({view = Var "List.hd";_}, [{view = FieldOf (_, "buys", _);_}]) -> mk ~ty:x.ty (Var "First buy order")
| Funcall ({view = Var "List.hd";_}, [{view = FieldOf (_, "sells", _);_}]) -> mk ~ty:x.ty (Var "First sell order")
| Funcall ({view = Var "List.hd";_}, [{view = Funcall ({view = Var "List.tl";_}, [{view = FieldOf (_, "buys", _);_}]);_}]) -> mk ~ty:x.ty (Var "Second buy order")
| Funcall ({view = Var "List.hd";_}, [{view = Funcall ({view = Var "List.tl";_}, [{view = FieldOf (_, "sells", _);_}]);_}]) -> mk ~ty:x.ty (Var "Second sell order")
| Is (t, ty, {view = FieldOf (_, "order_type", x);_}) -> mk ~ty:x.ty (Is (t, ty, x))
| FieldOf (Record, (("order_id" | "order_qty" | "order_price" | "order_time") as field), x)
-> mk ~ty:x.ty (FieldOf(Human, field, x))
| _ -> x
let refine node =
XF.walk_fix walk node
|> CCList.return
end
let pp_cs ?inv cs =
cs
|> PPrinter.pp ~refine:Refiner.refine ?inv
|> List.map (CCFormat.to_string (PPrinter.Printer.print ()))
let regions_doc d =
Jupyter_imandra.Decompose_render.regions_doc ~pp_cs d;;
#install_doc regions_doc;;
Now we see the same regions, but constraints and invariants refined and translated into English-like prose. Notice that references to the OCaml function List.hd have been replaced by First Buy Order, just as we've wanted.
Adding constraints (side conditions)¶
The regions Imandra has thus far produced describe the full state-space of match_price. But what if we would like to focus on its specific subset? Can we, somehow, 'slice' the state-space? Absolutely, you can do this by adding a 'side-condition', a function that takes the same arguments as match_price and returns a Boolean value. Imandra will constrain the state-space of match_price such that the side condition is true. This is quite a powerful mechanism which we'll illustrate with two examples: one case where we simply constrain the inputs into match_price and another where we constrain the output of match_price:
(* Side condition function must be defined in logic mode just like the original `match_price` function. *)
#logic;;
let side_condition (ob : order_book) (ref_price : real) =
match best_buy(ob), best_sell(ob) with
| Some bb, Some bs ->
bb.order_type = Market && bs.order_type = Market
| _ -> false
;;
(* Decomposition is a `program-mode` feature allowing us to use any OCaml/ReasonML code to manipulate the results. *)
#program;;
Modular_decomp.(top ~assuming:"side_condition" "match_price" |> get_concrete);;
All of the newly generated regions now contain the constraints that there's at least a single order on both sides of the book and that both of those orders are Market.
Let us now constrain the behaviour to only that which produces a Known _ type of fill price. Notice that now we will constrain the output of match_price. (OCaml-specific note: we use _ as a symbolic placeholder to indicate that we're not fixing it to be something specific)
(* Again, we need to switch back to logic mode so the engine translates the definition into axiomatic representation. *)
#logic;;
let side_condition2 (ob : order_book) (ref_price : real) =
match match_price ob ref_price with
| Known _ -> true
| Unknown -> false
;;
#program;;
Modular_decomp.(top ~assuming:"side_condition2" "match_price" |> get_concrete)
Generating instances¶
In our last step, we'll ask Imandra to synthesize concrete examples for each of the regions it generates. We'll generate just one for each region, but the interface is generic so you can request as many as you'd like. Moreover, since these values are valid OCaml (or ReasonML), you can directly compute with them or convert into whatever format you'd like (e.g. as FIX messages).
The first step will create a new module for us which we'll use in the second step to query for sample points.
(* Generate a model extractor module for `match_price` *)
Extract.eval ~signature:(Event.DB.fun_id_of_str (db()) "match_price") ();;
(* Let's now extract test cases from each region *)
Modular_decomp.get_regions d
|> CCList.map (fun r -> r |> Modular_decomp.get_model |> Mex.of_model)
If you have any questions, please don't hestitate to reach out to us via email or on our Discord server.

