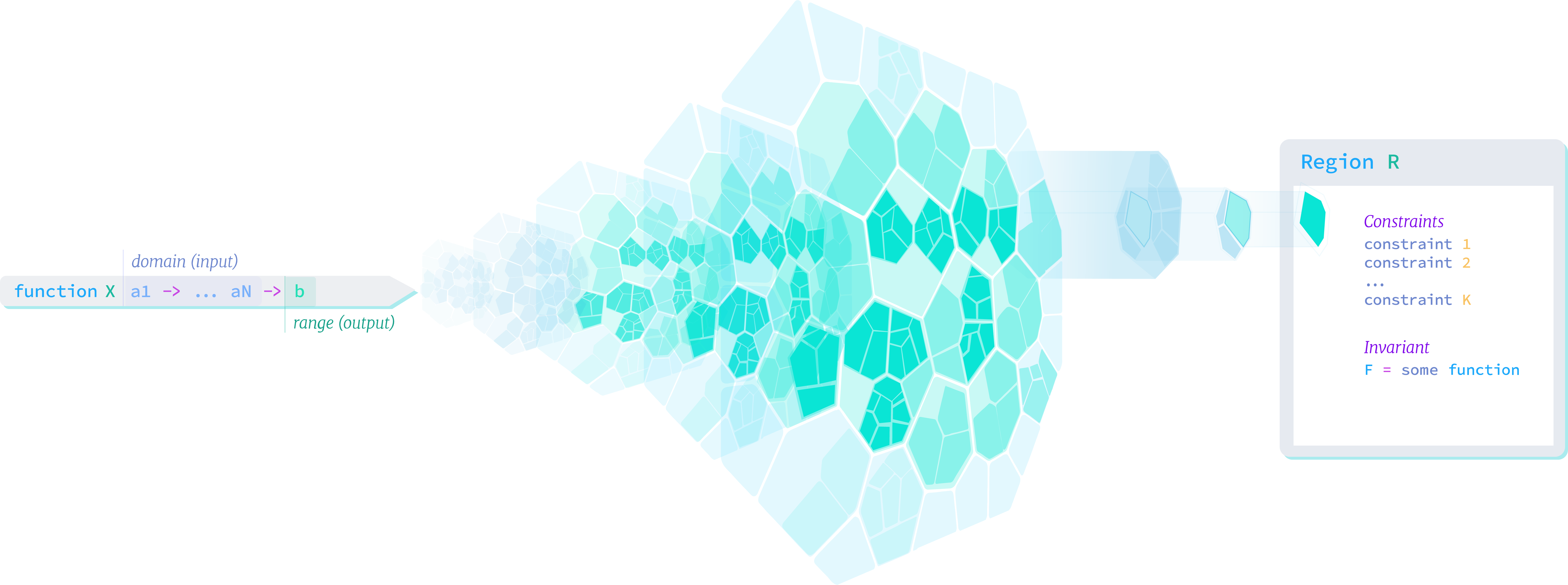
Region decomposition lifts Cylindrical Algebraic Decomposition (CAD) to algorithms through a combination of symbolic execution, automated induction and nonlinear decision procedures. The result is an automatic method for decomposing the state-space of a system (as given by the “step” function of an (infinite) state-machine) into a finite number of symbolically described regions s.t. (a) the union of all regions covers the entire state-space, and (b) in each region, the behavior of the system is invariant. Regions decompositions are computed subject to a basis, a collection of function and predicate symbols which are taken as “basic” and will be used in region descriptions, and side-conditions which may express queries to focus the decomposition on specific behaviors (i.e., compute all regions of the state-space s.t. the controller will result in the following bad state). Bases and side-conditions facilitate configurable abstraction boundaries and foci and allow the analysis of the state-space to be adapted for many different applications, from high-coverage test-suite generation to automated documentation synthesis to interactive state-space exploration.

