Proving Program Termination¶
In this notebook, we'll walk through how Imandra can be used to analyse program termination. Along the way, we'll learn about soundness, conservative extensions, the Halting Problem, ordinals (up to $\epsilon_0$!) and well-founded orderings, path-guarded call-graphs, measure conjectures and more.
Before we dive into discussing (relatively deep!) aspects of mathematical logic, let's begin with a simple example. What happens when we try to define a non-terminating recursive function in Imandra?
As we can see, Imandra rejects this definition of f given above. Contrast this with a definition of a function like map:
Imandra accepts our function map and proves it terminating. Under the hood, Imandra uses ordinals in its termination analyses, beautiful mathematical objects representing equivalence classes of well-orderings. We'll discuss these more below!

Before we do so, let's return to that function f that Imandra rejected.
Inconsistent non-terminating functions¶
Imagine if Imandra allowed every possible recursive function to be admitted into its logic, even those that didn't terminate. If that were the case, we could easily define the following function:
let rec f x = f x + 1 (note the binding strength of f, i.e., this is equivalent to let rec f x = (f x) + 1)
With this function admitted, we could then use its defining equation f x = f x + 1 to derive a contradiction, e.g., by subtracting f x from both sides to derive 0 = 1:
f x = f x + 1
f x - f x = f x + 1 - f x
0 = 1
This inconsistency arises because, actually, such a function f cannot "exist"!
You may be wondering: Why does consistency matter?
Soundness, Consistency and Conservative Extensions¶
Imandra is both a programming language and a logic. A crucial property of a logic is soundness. For a logic to be sound, every theorem provable in the logic must be true. An unsound theorem prover would be of little use!
As we're developing programs and reasoning about them in Imandra, we're extending Imandra's logical world by defining types, functions, modules, and proving theorems. At any given time, this collection of all definitions and theorems is referred to as Imandra's current theory. It's important to ensure this current theory T is consistent, i.e., that there exists no statement P such that both P and (not P) are provable from T. If we weren't sure if T were consistent, then we would never know if a "theorem" was provable because it was true, or simply because T proves false (and false implies everything!).
Imandra's definitional principle is designed to ensure this consistency, by enforcing certain restrictions on our definitions. In the parlance of mathematical logic, Imandra's definitional principle ensures that every definitional extension of Imandra's current theory is a conservative extension.
There are two main rules Imandra enforces for ensuring consistency:
- Every defined type must be well-founded.
- Every defined function must be total (i.e., terminating on all possible inputs).
In this notebook, we'll focus on the latter: proving program termination!
Termination ensures existence¶
Thankfully, a deep theorem of mathematical logic tells us that admitting terminating (also known as total) functions cannot lead us to inconsistency.
To admit a new function into Imandra's logic, Imandra must be able to prove that it always terminates. For most common patterns of recursion, Imandra is able to prove termination automatically. For others, users may need to give Imandra help in the form of hints and measures.
Let's get our hands dirty¶
Let's define a few functions and see what this is like. First, let's observe that non-recursive functions are always admissible (provided we're not dealing with redefinition):
Let's now define some simple recursive functions, and observe how Imandra responds.
Out of curiosity, let's see what would happen if we made a mistake in our definition of sum above, by, e.g., using x = 0 as our test instead of x <= 0:
Note how Imandra rejects the definition, and tells us this is because it could not prove termination, in particular regarding the problematic recursive call sum_oops (x-1). Indeed, sum_oops does not terminate when x is negative!
Structural Recursions¶
Structural recursions are easy for Imandra. For example, let's define a datatype of trees and a few functions on them. Imandra will fly on these termination proofs.
For fun, let's ask Imandra to synthesize an int tree of size 5 for us:
Cool! Let's now define a function to sum the leaves of an int tree:
let rec sum_tree = function
| Leaf n -> n
| Node (a,b) -> sum_tree a + sum_tree b
Out of curiosity, are there any trees whose size is greater than 5 and equal to 3 times their sum?
Yes! Let's compute with that counterexample to see:
Ackermann and Admission Hints¶
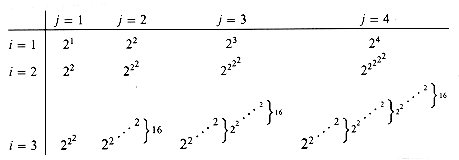
The Ackermann function (actually, family of functions) is famous for many reasons. It grows extremely quickly, so quickly that it can be proved to not be primitive recursive!
Here's an example definition:
let rec ack m n =
if m <= 0 then n + 1
else if n <= 0 then ack (m-1) 1
else ack (m-1) (ack m (n-1))It's worth it to study this function for a bit, to get a feel for why its recursion is tricky.
If we ask Imandra to admit it, we find out that it's tricky for Imandra, too!
let rec ack m n =
if m <= 0 then n + 1
else if n <= 0 then ack (m-1) 1
else ack (m-1) (ack m (n-1))
Imandra tells us that it's unable to prove termination in the particular path that goes from ack m n to ack m (n-1). Imandra further tells us that it tried to prove termination in this case using a measured subset of the arguments of ack containing only m.
Why does ack terminate, and how can we explain this to Imandra?
If we think about it for a little bit, we realise that ack terminates because its pair of arguments decreases lexicographically in its recursive calls. From the perspective of ordinals, the arguments of the recursive calls decrease along the ordinal $\omega^2$.
Lexicographic termination (up to $\omega^\omega$)¶
Lexicographic termination is so common, there's a special way we can tell Imandra to use it.
This is done with the @@adm ("admission") attribute.
We can tell Imandra to prove ack terminating by using a lexicographic order on (m,n) in the following way:
let rec ack m n =
if m <= 0 then n + 1
else if n <= 0 then ack (m-1) 1
else ack (m-1) (ack m (n-1))
[@@adm m,n]
Success! You may enjoy walking through Imandra's termination proof presented in the document above.
Measures and Ordinals¶
If a lexicographic ordering isn't sufficient to prove termination for your function, you may need to construct a custom measure function.
A measure function is ordinal valued, meaning it returns a value of type Ordinal.t.
Imandra's Ordinal module comes with helpful tools for constructing ordinals.
Let's view its contents with the #show directive:
Even though ordinals like $\omega$ are infinite, we may still compute with them in Imandra.
Ordinals are fundamental to program termination because they represent well-founded orderings (well-orders).
If we can prove that a function's recursive calls always get smaller with respect to some well-founded ordering, then we know the function will always terminate.
The fundamental well-founded relation in Imandra is Ordinal.(<<). This is the strict, well-founded ordering relation on the ordinals up to $\epsilon_0$:
Let's consider an example famous recursive function that we can't admit with a lexicographic order and see how we can write our own measure function and communicate it to Imandra.
Left pad¶
Consider the following function left_pad:
let rec left_pad c n xs =
if List.length xs >= n then
xs
else
left_pad c n (c :: xs)If we give this function to Imandra without any hints, it will not be able to prove it terminating.
let rec left_pad c n xs =
if List.length xs >= n then
xs
else
left_pad c n (c :: xs)
Why does this function terminate? If we think about it, we can realise that it terminates because in each recursive call, the quantity n - List.length xs is getting smaller. Moreover, under the guards governing the recursive calls, this quantity is always non-negative. So, let's construct an ordinal-valued measure function to express this:
We can compute with this function, to really see it does what we want:
Finally, we can give it to Imandra as the measure to use in proving left_pad terminates:
let rec left_pad c n xs =
if List.length xs >= n then
xs
else
left_pad c n (c :: xs)
[@@measure left_pad_measure n xs]
Success! Note also how we only used two of left_pad's three arguments in our measure. In general, economical measures are good, as they give us smaller measured subsets, which allow us to simplify more symbolic instances of our recursive functions during proof search. Moreover, they also affect how Imandra is able to use its functional induction (a.k.a. recursion induction) schemes.
We can find out the measured subset (and much other data) about our functions through the #history directive. It's also available with the handy alias #h:
Excellent! This concludes our brief introduction to program termination in Imandra.


